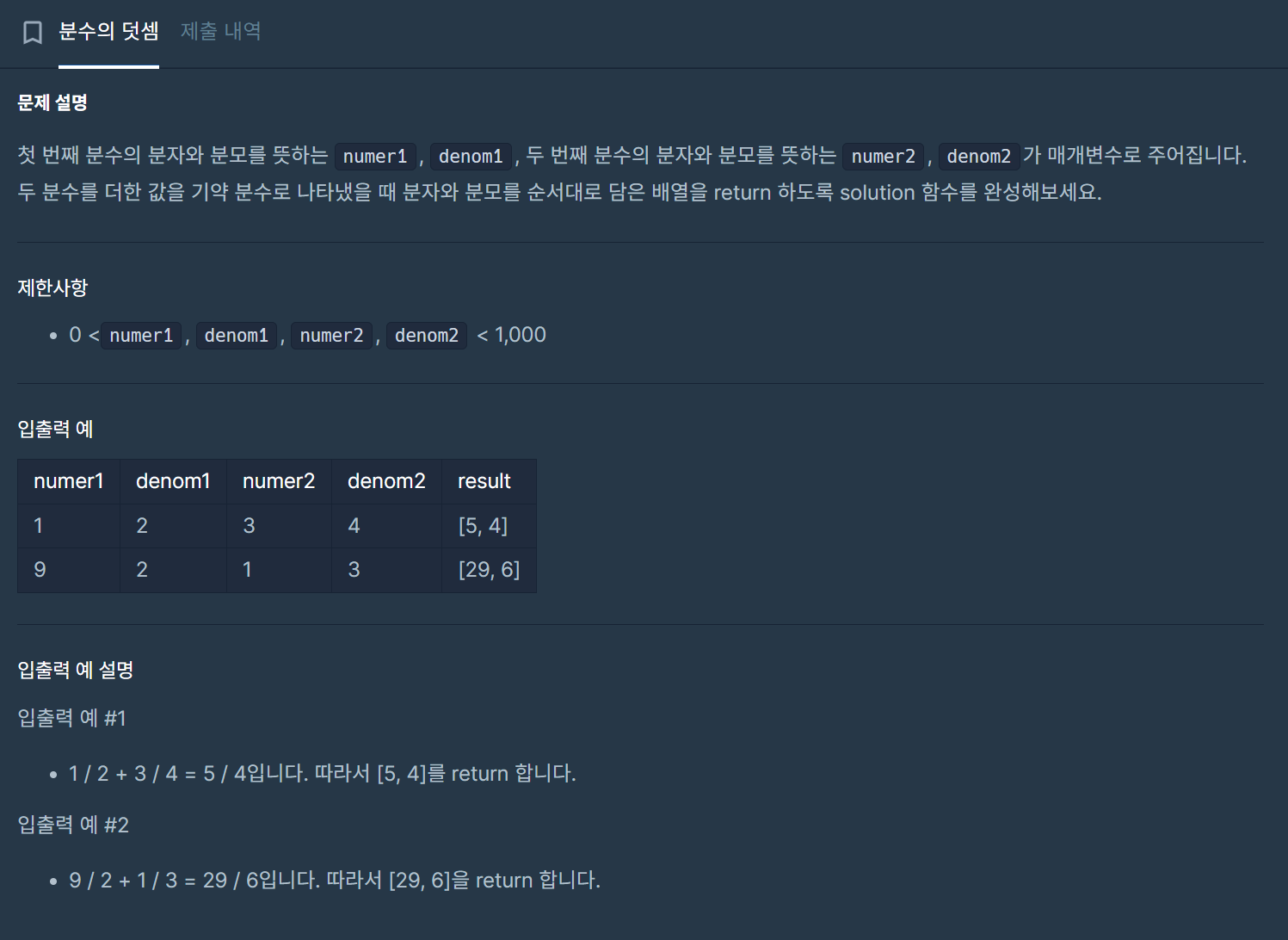
문제
https://school.programmers.co.kr/learn/courses/30/lessons/120808
풀이
class Solution {
public int[] solution(int numer1, int denom1, int numer2, int denom2) {
// 1️⃣ 분수 덧셈: 통분
// a/b + c/d = (a*d + b*c) / (b*d)
int numerator = numer1 * denom2 + numer2 * denom1; // 분자 계산
int denominator = denom1 * denom2; // 분모 계산
// 2️⃣ 최대공약수(GCD) 계산
int gcd = getGCD(numerator, denominator);
// 3️⃣ 기약분수로 만들기: 분자와 분모를 GCD로 나누기
numerator /= gcd;
denominator /= gcd;
// 4️⃣ 결과 배열 반환
return new int[]{numerator, denominator};
}
// ✅ 최대공약수(GCD) 계산: 유클리드 호제법
// 원리: GCD(a, b) = GCD(b, a % b), b가 0이면 a가 GCD
private int getGCD(int a, int b) {
while (b != 0) { // b가 0이 될 때까지 반복
int temp = a % b; // a를 b로 나눈 나머지를 temp에 저장
a = b; // a 자리에 b를 넣음
b = temp; // b 자리에 나머지를 넣음
// 반복하며 계속 나머지 계산 → 나중에 b가 0이 되면 a가 GCD
}
return a; // b가 0이 되면 최대공약수 반환
}
}class Solution {
public int[] solution(int numer1, int denom1, int numer2, int denom2) {
// 1️⃣ 분수 덧셈: 통분
int n = numer1 * denom2 + numer2 * denom1; // 분자
int d = denom1 * denom2; // 분모
int g; // 최대공약수 저장 변수
// 2️⃣ 최대공약수(GCD) 구하기: 반복문 사용
// 1) n과 d 중 큰 수부터 1까지 내려가며
// 2) n과 d를 모두 나누어 떨어뜨리는 수를 찾음
for (g = (n > d ? n : d); g > 0; g--) {
if (n % g == 0 && d % g == 0) { // n과 d 모두 나누어 떨어지는 g 찾음
break; // 최대공약수 발견 시 반복 종료
}
}
// 3️⃣ 기약분수로 만들기
return new int[]{n / g, d / g}; // 분자, 분모를 GCD로 나눠 반환
}
}import java.util.function.BiFunction;
class Solution {
public int[] solution(int numer1, int denom1, int numer2, int denom2) {
// 1️⃣ 람다로 유클리드 호제법 구현
// BiFunction<Integer, Integer, Integer> : 두 Integer 입력 -> Integer 반환
BiFunction<Integer, Integer, Integer> gcd = new BiFunction<>() {
@Override
public Integer apply(Integer a, Integer b) {
// 재귀: b가 0이면 a 반환, 아니면 GCD(b, a % b) 호출
return b == 0 ? a : this.apply(b, a % b);
}
};
// 2️⃣ 분수 덧셈: 통분
int n = numer1 * denom2 + numer2 * denom1; // 분자 계산
int d = denom1 * denom2; // 분모 계산
// 3️⃣ GCD 계산 후 기약분수 만들기
int g = gcd.apply(n, d); // 람다를 사용해 GCD 계산
return new int[]{n / g, d / g}; // 분자와 분모를 GCD로 나눠 반환
}
}'Algorithm > Programmers' 카테고리의 다른 글
| [Programmers] Lv.0 | 두 수의 나눗셈 | Java (0) | 2025.11.05 |
|---|---|
| [Programmers] Lv.0 | 숫자 비교하기 | Java (0) | 2025.11.05 |
| [Programmers] Lv.0 | 배열 두 배 만들기 | Java (0) | 2025.11.05 |
| [Programmers] Lv.0 | 나머지 구하기 | Java (0) | 2025.11.05 |
| [Programmers] Lv.0 | 중앙값 구하기 | Java (0) | 2025.11.05 |




댓글