https://www.acmicpc.net/problem/11729
11729번: 하노이 탑 이동 순서
세 개의 장대가 있고 첫 번째 장대에는 반경이 서로 다른 n개의 원판이 쌓여 있다. 각 원판은 반경이 큰 순서대로 쌓여있다. 이제 수도승들이 다음 규칙에 따라 첫 번째 장대에서 세 번째 장대로
www.acmicpc.net

주의점
- Scanner + System.out.println(): 시간 초과 에러 발생
알고리즘
재귀 핵심 순서
- 일정 규칙 찾기 ➡ 최소 단위에서 적용
- 재귀를 통해 '가장 작은 단위'가 될 때까지 재귀 호출 반복
- 가장 작은 단위까지 호출되면 그 지점에서 구현한 연산 실행
하노이의 탑



핵심 규칙
- 큰 원판이 작은 원판 위에 있어서는 안 됨
하노이의 탑 풀이
n개의 원판이 있다고 가정

1. 가장 큰 원판을 C로 옮기기 위해 (n - 1)개의 원판이 A에서 B로 가야함
- B로 이동하기 위해 (n - 1)번 만큼 반복
- A에서 B로 가는 것 = Hanoi 함수
- (n - 1)개 만큼 반복한다는 의미
∴ 이동 횟수 : Hanoi (n - 1)

2. A에 있는 가장 큰 원판이 C로 이동
- 가장 큰 원판만 이동하기에 횟수는 1회
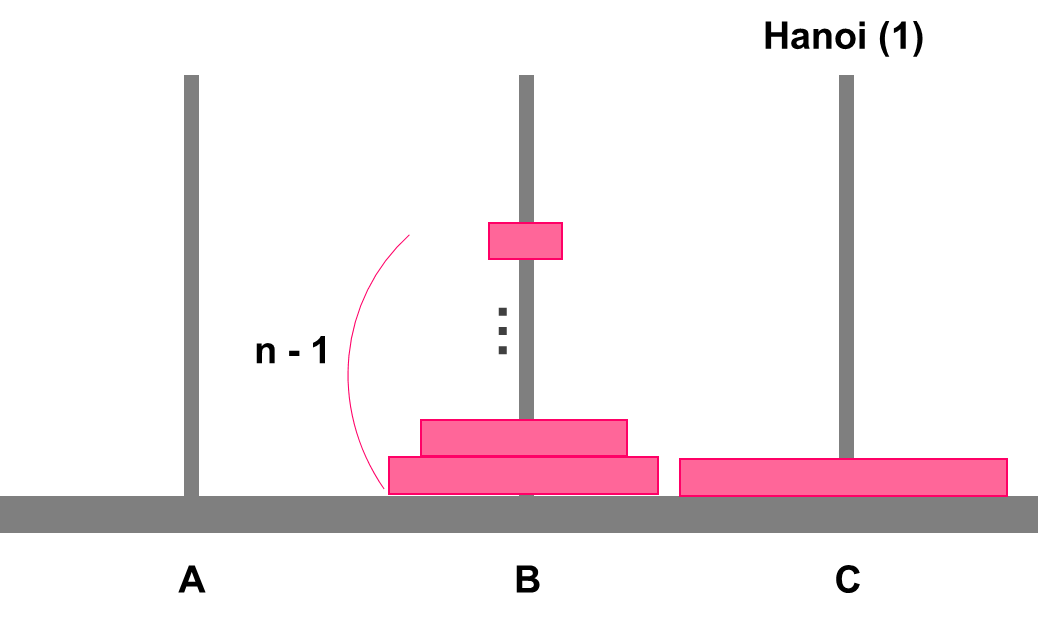
3. B에 있는 (n - 1)개의 원판을 C로 이동
- 이전 단계에서 A에서 B로 (n - 1)개 이동하듯, B에서 C로 이동하는 횟수는 Hanoi (n - 1)이 됨

정리
- n개의 원판을 이동시키기 위해 Hanoi (n - 1) 횟수 만큼 2번 이동
- 가장 아래 원판은 1번 이동
Hanoi (n) = 2 x Hanoi (n - 1) + 1
수학적 풀이
- n개의 원판을 이동시키기 위한 이동 횟수 : an
- n개의 원판을 옮기려면 그 위에 위치한 (n - 1)개의 원판을 모두 다른 막대로 옮긴 후,
- 맨 아래 원판을 빈 막대로 옮긴 뒤, 그 위에 (n - 1)개의 원판을 옮겨놓아야 함
원판이 이동하는 점화식


귀납적 정리

첫 번째 줄에 출력해야 할 원판 이동 횟수 공식

풀이
1. Scanner + StringBuilder()
import java.util.Scanner;
public class Main {
public static StringBuilder sb = new StringBuilder();
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int N = in.nextInt();
sb.append((int) (Math.pow(2, N) - 1)).append('\n');
Hanoi(N, 1, 2, 3);
System.out.println(sb);
}
/*
N: 원판의 개수
start: 출발지
mid: 옮기기 위해 이동해야 장소
to: 목적지
*/
public static void Hanoi(int N, int start, int mid, int to) {
//이동할 원반의 수가 1개일 때
if (N == 1) {
sb.append(start + " " + to + "\n");
return;
}
//A ➡ C로 옮긴다 가정할 때
//(N - 1)개를 A ➡ B로 이동(= start 지점의 (N - 1)개의 원판을 mid 지점으로 이동)
Hanoi(N - 1, start, to, mid);
//1개를 A ➡ C로 이동(= start 지점의 N 번째 원판을 to지점으로 이동)
sb.append(start + " " + to + "\n");
//(N - 1)개를 B ➡ C로 이동(= mid 지점의 (N - 1)개의 원판을 to 지점으로 이동)
Hanoi(N - 1, mid, start, to);
}
}
2. Scanner + BufferedWriter
import java.util.Scanner;
import java.io.BufferedWriter;
import java.io.OutputStreamWriter;
import java.io.IOException;
public class Main {
static BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
public static void main(String[] args) throws IOException {
Scanner in = new Scanner(System.in);
int N = in.nextInt();
bw.write((int) (Math.pow(2, N) - 1) + "\n");
Hanoi(N, 1, 2, 3);
bw.flush();
bw.close();
}
/*
N: 원판의 개수
start: 출발지
mid: 옮기기 위해 이동해야 장소
to: 목적지
*/
public static void Hanoi(int N, int start, int mid, int to) {
//이동할 원반의 수가 1개일 때
if (N == 1) {
sb.append(start + " " + to + "\n");
return;
}
//A ➡ C로 옮긴다 가정할 때
//(N - 1)개를 A ➡ B로 이동(= start 지점의 (N - 1)개의 원판을 mid 지점으로 이동)
Hanoi(N - 1, start, to, mid);
//1개를 A ➡ C로 이동(= start 지점의 N 번째 원판을 to지점으로 이동)
sb.append(start + " " + to + "\n");
//(N - 1)개를 B ➡ C로 이동(= mid 지점의 (N - 1)개의 원판을 to 지점으로 이동)
Hanoi(N - 1, mid, start, to);
}
}3. BufferedReader + StringBuilder()
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.IOException;
public class Main {
public static StringBuilder sb = new StringBuilder();
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
sb.append((int) (Math.pow(2, N) - 1)).append('\n');
Hanoi(N, 1, 2, 3);
System.out.println(sb);
}
/*
N: 원판의 개수
start: 출발지
mid: 옮기기 위해 이동해야 장소
to: 목적지
*/
public static void Hanoi(int N, int start, int mid, int to) {
//이동할 원반의 수가 1개일 때
if (N == 1) {
sb.append(start + " " + to + "\n");
return;
}
//A ➡ C로 옮긴다 가정할 때
//(N - 1)개를 A ➡ B로 이동(= start 지점의 (N - 1)개의 원판을 mid 지점으로 이동)
Hanoi(N - 1, start, to, mid);
//1개를 A ➡ C로 이동(= start 지점의 N 번째 원판을 to지점으로 이동)
sb.append(start + " " + to + "\n");
//(N - 1)개를 B ➡ C로 이동(= mid 지점의 (N - 1)개의 원판을 to 지점으로 이동)
Hanoi(N - 1, mid, start, to);
}
}
4. BufferedReader + BufferedWriter
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.IOException;
import java.io.BufferedWriter;
import java.io.OutputStreamWriter;
public class Main {
static BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
bw.write((int) (Math.pow(2, N) - 1) + "\n");
Hanoi(N, 1, 2, 3);
bw.flush();
bw.close();
}
/*
N: 원판의 개수
start: 출발지
mid: 옮기기 위해 이동해야 장소
to: 목적지
*/
public static void Hanoi(int N, int start, int mid, int to) {
//이동할 원반의 수가 1개일 때
if (N == 1) {
sb.append(start + " " + to + "\n");
return;
}
//A ➡ C로 옮긴다 가정할 때
//(N - 1)개를 A ➡ B로 이동(= start 지점의 (N - 1)개의 원판을 mid 지점으로 이동)
Hanoi(N - 1, start, to, mid);
//1개를 A ➡ C로 이동(= start 지점의 N 번째 원판을 to지점으로 이동)
sb.append(start + " " + to + "\n");
//(N - 1)개를 B ➡ C로 이동(= mid 지점의 (N - 1)개의 원판을 to 지점으로 이동)
Hanoi(N - 1, mid, start, to);
}
}성능
- BufferedReader > Scanner
- StringBuilder: 더 많은 메모리 차지하나, 상황에 따라 BufferedWriter보다 성능 better
'Algorithm > Baekjoon' 카테고리의 다른 글
| [백준] 2231번 : 분해합 - Java (0) | 2022.04.12 |
|---|---|
| [백준] 2798번 : 블랙잭 - Java (0) | 2022.04.12 |
| [백준] 2447번 : 별 찍기 - 10 - Java (0) | 2022.04.06 |
| [백준] 10870번 : 피보나치 수 5 - Java (0) | 2022.04.05 |
| [백준] 1002번 : 터렛 - Java (0) | 2022.04.04 |




댓글